问题
填空题
曲线y＝x-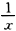
与x轴交点处的切线方程为（）
答案
参考答案：2x-y-2＝0，2x-y+2＝0．
解析：
先求曲线y＝x-
与x轴的交点：由x-＝0，得交点坐标为(-1，0)和(1，0)．又 所以，过点(-1，0)的切线方程为： y＝2(x+1)，即2x-y+2＝0 过点(1，0)的切线方程为： y＝2(x-1)，即2x-y-2＝0．
搜题请搜索小程序“爱下问搜题”
曲线y＝x-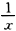与x轴交点处的切线方程为（）
参考答案：2x-y-2＝0，2x-y+2＝0．
解析：
先求曲线y＝x-与x轴的交点：由x-＝0，得交点坐标为(-1，0)和(1，0)．又 所以，过点(-1，0)的切线方程为： y＝2(x+1)，即2x-y+2＝0 过点(1，0)的切线方程为： y＝2(x-1)，即2x-y-2＝0．