问题
单项选择题
已知a，b，c为正数，若一元二次方程ax2+bx+c＝0有两个不等实根，则方程a2x2+b2x+c2＝0（）．
A．有两个不等的正根
B．有两个不等的负根
C．有一个正根，一个负根
D．没有实根
答案
参考答案：B
解析：
由已知，有b2-4ac＞0，即b2＞4ac．于是b4＞16a2c2＞4a2c2．故b4- 4a2c2＞0．从而方程a2x2+b2x+c2＝0有两个不等实根x1，x2．又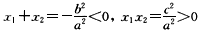
可知x1，x2均为负根．