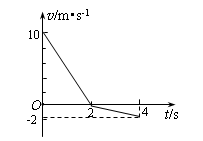
问题
填空题
正方形ABCD,E为正方形对角线交点,将正方形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,有如下四个结论:
①AB∥CD;②AC⊥BD;③△ACD是等边三角形;④平面AEC⊥平面BCD.其中正确的结论是______.
答案
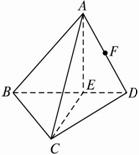
由已知可得AB∩平面BCD=B,B?CD
故AB与CD异面,故①错误
取BD的中点E,则AE⊥BD,CE⊥BD.
∴BD⊥面AEC.
∴BD⊥AC,故②正确.
设正方形边长为a,则AD=DC=a,AE=
a=EC.2 2
∴AC=a.
∴△ACD为等边三角形,故③正确
∵AB=AD,E为BD中点,
∴AE⊥BD,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AE?平面ABD
故AE⊥平面BCD,
又∵AE?平面AEC
∴平面AEC⊥平面BCD,故④正确;
故答案为:②③④