问题
单项选择题
如0<α<β<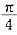 ,sinα+cosα=a,sinβ+cosβ=b,则()。
,sinα+cosα=a,sinβ+cosβ=b,则()。
A.a<b
B.a>b
C.ab<1
D.ab>2
答案
参考答案:A
解析:
(sinα+cosα)2=1+2sin2α=a2,(sinβ+cosβ)2=1+2cos2β=b2,又0<2α<2β<,故sin2α<sin2β,从而a2<b2,又a,b>0,则a<b,选(A).
如0<α<β<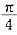 ,sinα+cosα=a,sinβ+cosβ=b,则()。
,sinα+cosα=a,sinβ+cosβ=b,则()。
A.a<b
B.a>b
C.ab<1
D.ab>2
参考答案:A
解析:
(sinα+cosα)2=1+2sin2α=a2,(sinβ+cosβ)2=1+2cos2β=b2,又0<2α<2β<,故sin2α<sin2β,从而a2<b2,又a,b>0,则a<b,选(A).