（1）当b＜0时，f（x）=|x|x+bx+c=

x2+bx+c  ，x≥0  -x2+bx+c，x＜0

值域是R，故函数f（x）在R上没有最小值；
（2）当b＞0时，f（x）=|x|x+bx+c=

x2+bx+c  ，x≥0  -x2+bx+c，x＜0

，知函数f（x）在R上是单调增函数；
（3）若f（x）=|x|x+bx那么函数f（x）是奇函数（f（-x）=-f（x）），也就是说函数f（x）的图象关于（0，0）对称．而函数f（x）=|x|x+bx+c的图象是由函数f（x）=|x|x+bx的图象沿Y轴移动，故图象一定是关于（0，c）对称的．

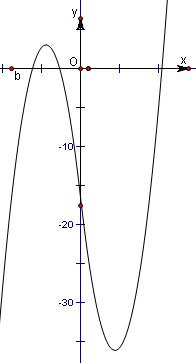
（4）当b＜0时，方程f（x）=0有三个不同实数根，考虑函数f（x）与x轴有三个交点，如图，

其充要重要条件是函数y=f（x）的极大值大于0且极小值小于0，

即b²-4c＞0，b²＞4|c|；

故（4）正确；

（5）f（x）=|x|x+bx+c=

x2+bx+c  ，x≥0  -x2+bx+c，x＜0

的每一段分段函数的图象都是一个二次函数的部分图象，且它们有一个公共点（0，c），由图角可得解得方程f（x）=0最多有三个不同的实根，不可能有四个不同实数根．所以（5）不正确．

故答案为：（2）（3）（4）．