问题
填空题
已知定义在R上的偶函数满足:f(x+4)=f(x)+f(2),且当x∈[0,2]时,y=f(x)单调递减,给出以下四个命题:
①f(2)=0;
②x=-4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]单调递增;
④若方程f(x)=m在[-6,-2]上的两根为x1,x2,则x1+x2=-8.
上述命题中所有正确命题的序号为______.
答案
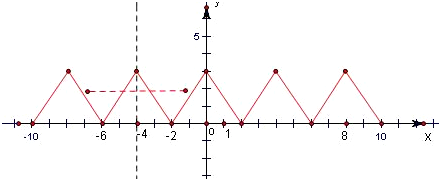
∵f(x)是定义在R上的偶函数,
∴f(-x)=f(x),
可得f(-2)=f(2),
在f(x+4)=f(x)+f(2),中令x=-2得
f(2)=f(-2)+f(2),
∴f(-2)=f(2)=0,
∴f(x+4)=f(x),∴函数f(x)是周期为4的周期函数,又当x∈[0,2]时,y=f(x)单调递减,结合函数的奇偶性画出函数f(x)的简图,如图所示.
从图中可以得出:
②x=-4为函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[8,10]单调递减;
④若方程f(x)=m在[-6,-2]上的两根为x1,x2,则x1+x2=-8.
故答案为:①②④.
