阅读下列说明和C代码，回答问题1至问题3，将解答写在对应栏内。

[说明]

对有向图进行拓扑排序的方法如下。

(1)初始时拓扑序列为空。

(2)任意选择一个入度为0的顶点，将其放入拓扑序列中，同时从图中删除该顶点以及从该顶点出发的弧。

(3)重复(2)，直到不存在入度为0的顶点为止(若所有顶点都进入拓扑序列，则完成拓扑排序；否则，由于有向图中存在回路无法完成拓扑排序)。

函数int* TopSort(LinkedDigraph G)的功能是对有向图G中的顶点进行拓扑排序，返回拓扑序列中的顶点编号序列，若不能完成拓扑排序，则返回空指针。其中，图G中的项点从1开始依次编号，顶点序列为v1，v2，…，vn，图G采用邻接表表示，其数据类型定义如下：

#define MAXVNUM 50 /*最大顶点数*/

typedef struct ArcNode /*表结点类型*/

int adjvex； /*邻接顶点编号*/

Struct ArcNode *nextarc； /*指示下一个邻接顶点*/

ArcNode；

typedef struct AdjList /*头结点类型*/

char vdata； /*顶点的数据信息*/

ArcNode *firstarc； /*指向邻接表的第一个表结点*/

AdjList；

typedef struct LinkedDigraph /*图的类型*/

int n； /*图中顶点个数*/

AdjList Vhead[MAXVNUM]； /*所有顶点的头结点数组*/

LinkedDigraph；

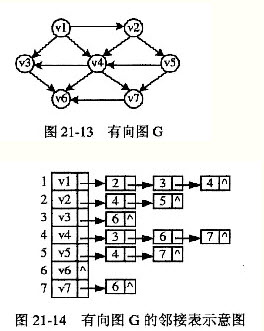
例如，某有向图G如图21-13所示，其邻接表如图21-14所示。

函数TopSort中用到了队列结构(Queue的定义省略)，实现队列基本操作的函数原型如表21-4所示。

[C代码]

int *TopSort；(LinkedDigraph G)

ArcNode *p； /*临时指针，指示表结点*/

Queue Q； /*临时队列，保存入度为0的顶点编号*/

int k=0； /*临时变量，用作数组元素的下标*/

int j=0，w=0； /*临时变量，用作顶点编号*/

int *topOrder，*inDegree；

topOrder=(int *)malloc((G.n+1) * sizeof(int))；/*存储拓扑序列中的顶点编号*/

inDegree=(int *)malloc((G.n+1) *siZeof(int))；/*存储图G中各顶点的入度*/

if(!inDegree || !topOrder)return NULL；

(1) ； /*构造一个空队列*/

for(j=1；j＜=G.n；j++) /*初始化*/

topOrder[j]=0； inDegree[j]=0；

for(j=1；j＜=G.n；j++) /*求图G中各顶点的入度*/

for(p=G.Vhead[j].firstarc；p；p=p-＞nextarc)

inDegree[p-＞adjvex]+=1；

for(j=1；j＜=G.n；j++) /*将图G中入度为0的顶点保存在队列中*/

if(0==inDegree[j]) EnQueue(＆Q，j)；

while(!IsEmpty(Q))

(2) ； /*队头顶点出队列并用W保存该顶点的编号*/

topOrder[k++]=w；

/*将顶点w的所有邻接顶点的入度减1(模拟删除顶点W及从该顶点出发的弧的操作)*/

for(p=G.Vhead[w].firstare；p；p=p-＞nextarc)

(3) -=1；

if(0== (4) ) EnQueue(＆Q，p-＞adjvex)；

/*for*/

/*while*/

free(inDegree)；

if( (5) )

return NULL；

return topOrder；

/*TopSort*/

对于图21-13所示的有向图G，写出函数TopSort执行后得到的拓扑序列。若将函数TopSort中的队列改为栈，写出函数TopSort执行后得到的拓扑序列。