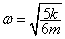问题
计算题
如图所示,在离心机的光滑水平横杆上穿着两个质量分别为2m和m的小球A和B,A、B间用劲度系数为k的轻弹簧连接,弹簧的自然长度为L,当 离心机以角速度ω转动时,欲使A、B两球仍能相对于横杆静止而又不碰到两侧挡板,已知两板间的距离为3L,求转速ω的最大值.
答案
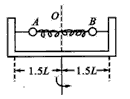
解:设转动的角速度为ω时,两球仍能相对横杆静止且半径较大的球刚好不碰挡板,则
2m·ω2rA =m·ω2rB,
即 rB=2rA.
表明当rB =1.5L时角速度最大,此时 0. 75L
0. 75L
故弹簧伸长量△x=rA +rB -L=1.25L.
对B:k△x =mω2rB,
联立上述各方程得