问题
计算题
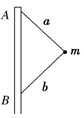
如图所示，把一个质量m＝1kg的物体通过两根等长的细绳与竖直杆上A、B两个固定点相连接，绳a、b长都是1m，杆AB长度是1.6m，直杆和球旋转的角速度等于多少时，b绳上才有张力？
答案
解：
如图所示，a、b两绳都伸直时，已知a、b绳长均为1m，
即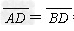
＝1 m，
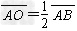＝0.8 m
在△AOD中，cosθ＝
＝0.8
sinθ＝0.6，θ＝37 °
小球做圆周运动的轨道半径r＝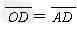
·sinθ＝1 ×0.6 m＝0.6 m.
b绳被拉直但无张力时，小球所受的重力mg与a绳拉力FTa的合力F为向心力，
其受力分析如图所示，由图可知小球的向心力为F＝mgtanθ
根据牛顿第二定律得F＝mgtanθ＝mrω2
解得直杆和球的角速度为ω＝
rad/s≈3.5 rad/s.
当直杆和球的角速度ω＞3.5 rad/s时，b中才有张力．