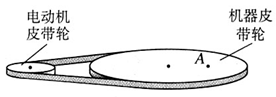
一部机器由电动机带动,机器上的皮带轮的半径是电动机皮带轮半径的3倍(如图),皮带与两轮之间不发生滑动。已知机器皮带轮边缘上一点的向心加速度为0.10 m/s2。
(1)电动机皮带轮与机器皮带轮的角速度之比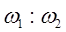 =?
=?
(2)机器皮带轮上A点到转轴的距离为轮半径的一半,A点的向心加速度是多少?
解:(1)因电动机和机器由同一皮带连接,所以它们边缘线速度相等设电动机半径为r1,角速度w1,机器轮半径为r2,角速度为w 2.
由题意知:r2 =3r1
由v=rw得 (3分)
r1w1 = r2w2
即 r1w1= 3r1w2
所以,
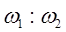 =3:1 ( 3分)
=3:1 ( 3分)
(2)因A与皮带边缘同轴转动,所以角速度相等,向心加速度与半径成正比,
由
a=rw2得 (2分)
aA=
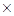 0.10 m/s2 ="0.05" m/s2 (2分)
0.10 m/s2 ="0.05" m/s2 (2分)
分析:传动装置,在传动过程中不打滑,则有:共轴的角速度是相同的;同一传动装置接触边缘的线速度大小是相等的.所以当角速度一定时,线速度与半径成正比;当线速度大小一定时,角速度与半径成反比.因此根据题目条件可知加速度及角速度关系.
解答:解:(1)因电动机和机器由同一皮带连接,所以它们边缘线速度相等设电动机半径为r1,角速度ω1,机器轮半径为r2,角速度为ω2.由题意知:r2=3r1
由v=rω得 r1ω1=r2ω2
即 r1ω1=3r1ω2
所以,ω1:ω2=3:1
(2)因A与皮带边缘同轴转动,所以角速度相等,向心加速度与半径成正比,
由a=rω2得 ,aA= ×0.10 m/s2=0.05 m/s2
×0.10 m/s2=0.05 m/s2
答:(1)电动机皮带轮与机器皮带轮的角速度之比ω1:ω2=3:1;
(2)机器皮带轮上A点到转轴的距离为轮半径的一半,A点的向心加速度是0.05 m/s2
点评:本题要紧扣隐含条件:共轴的角速度是相同的;同一传动装置接触边缘的线速度大小是相等的.以此作为突破口;同时能掌握线速度、角速度与半径之间的关系.
