问题
选择题
如图所示，A、B是两个摩擦传动轮，两轮半径大小关系为RA＝2RB，则两轮边缘上的
A．角速度之比ωA∶ωB＝2∶1
B．周期之比TA∶TB＝1∶2
C．转速之比nA∶nB＝1∶2
D．向心加速度之比aA∶aB＝2∶1
答案
答案：C
考点：
专题：计算题．
分析：解决本题的关键是两轮边缘上接触的地方线速度相等，然后根据角速度和线速度半径之间关系等求解．同时注意转速的物理意义，其在数值上和频率是相等的．
解答：解：两轮边缘的线速度相等，即vA=vB ①
线速度、角速度、半径关系为：v=ωr=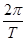
r=2πnr ②
向心加速度为：a=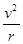
③
半径关系为：RA=2RB ④
联立①②③④可解得：ωA：ωB=1：2，TA：TB=2：1，nA：nB=1：2，aA：aB=1：2，故ABD错误，C正确．
故C正确．
点评：描述圆周运动的物理量较多如线速度、角速度、向心加速度、周期、频率、转速等，明确各物理量之间的关系，是解题的关键．