问题
计算题
如图所示,半径为R的光滑圆柱体被固定在水平平台上,圆柱体中心离台边水平距离为0.5R,质量为m1的小球用轻绳跨过圆柱与小球m2相连,开始时将m1控制住放在平台上,两边轻绳竖直。现在释放m1,让m1和m2分别由静止开始运动,当m1上升到圆柱体的最高点时,绳子突然断了,m1恰能做平抛运动,重力加速度为g。求:
(1)m1平抛时的速度v多大?
(2)m2应为m1的多少倍?
(3)m1做平抛运动的过程中,恰能经过与台面等高的B点,求B点离台边的距离sAB多大?

答案
解:(1)由牛顿第二定律:若m1恰能平抛,则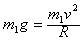
得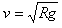
(2)当m1上升2R到圆柱体最高点时,m2下降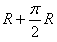
由机械能守恒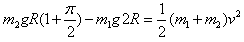
得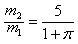
(3)平抛运动时间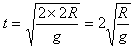
平抛水平距离x=vt=2R
离台边sAB=x-0.5R=1.5R