问题
解答题
求证:等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高.
答案
已知:△ABC中,AB=AC,D为BC上任意一点,DE⊥AB,DF⊥AC,垂足为E、F,
CG⊥AB于G,
求证:CG=DE+DF.

证明:已知如图所示.
∵ED⊥AB,
∴S△ABD=
AB?ED;1 2
∵DF⊥AC,
∴S△ACD=
AC?DF;1 2
∵CG⊥AB,
∴S△ABC=
AB?CG;1 2
又∵AB=AC,S△ABC=S△ABD+S△ACD,
∴
AB?CG=1 2
AB?ED+1 2
AC?DF,1 2
∴CG=DE+DF.

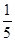 。造成这一现象的原因可能是
。造成这一现象的原因可能是