问题
解答题
证明：等腰三角形的两腰上的中线相等．
答案
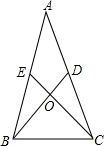
已知：等腰△ABC中，AB=AC，AD=DC，AE=EB，
求证：BD=CE．
证明：∵AB=AC，AD=DC，AE=EB，
∴DC=BE，∠DCB=∠EBC．
∵BC=CB，
∴△BDC≌△CEB（SAS）．
∴BD=CE．
即等腰三角形的两腰上的中线相等．
搜题请搜索小程序“爱下问搜题”
证明：等腰三角形的两腰上的中线相等．
已知：等腰△ABC中，AB=AC，AD=DC，AE=EB，
求证：BD=CE．
证明：∵AB=AC，AD=DC，AE=EB，
∴DC=BE，∠DCB=∠EBC．
∵BC=CB，
∴△BDC≌△CEB（SAS）．
∴BD=CE．
即等腰三角形的两腰上的中线相等．