问题
计算题
长度L=0.4m的细线，拴着一个质量m=0.4kg的小球，在竖直平面内作圆周运动，小球运动到最低点时离地面高度h=0.8m，此时细线受到的拉力F=13N，g取10m/s2，求：
（1）小球在最低点速度的大小；
（2）若小球运动到最低点时细线恰好断裂，则小球着地时速度为多大？
答案
解：（1）设最低点速度的大小为v，据牛顿第二定律得：F-mg=mv2/L
代入数据得v=3m/s
（2）小球运动到最低点时细线恰好断裂时有水平速度v=2m/s ，
小球做平抛运动，设小球下落时间t，由h=1/2gt2得t=0.4s。
小球竖直方向的速度vy=gt=4m/s
故小球着地时速度为v=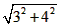
=5m/s。