问题
问答题
已知:正方体ABCD—A1B1C1D1,E为棱CC1的中点.
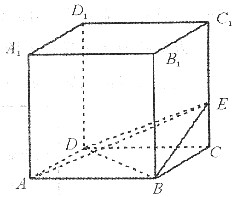
求证:AC∥平面B1DE.
答案
参考答案:
作BB1的中点F,连结AF、CF、EF.
∵E、F是CC1、BB1的中点,∴CE[*]B1F,
∴四边形B1FCE是平行四边形,∴CF∥B1E.
∵E,F是CC1、BB1的中点,∴EF[*]BC,
又BC[*]AD,∴EF[*]AD.
∴四边形ADEF是平行四边形,∴AF∥ED,
∵AF∩CF=F,B1E∩ED=E,
∴平面ACF∥面B1DE.
又AC[*]平面ACF,∴AC∥面B1DE.
