问题
填空题
△ABC中,AB=AC,∠BAC=90°,AD∥BC,BD=BC,∠DBC=______.
答案
(1)如图①;
过A作AE⊥BC于E,过D作DF⊥BC于F,则AE=DF;
∵△BAC是等腰直角三角形,
∴AE=
BC;1 2
∵BC=BD,
∴AE=DF=
BD;1 2
∴∠DBC=30°;
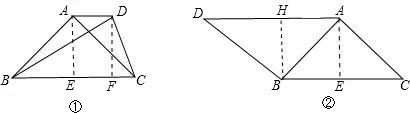
(2)如图②;
过A作AE⊥BC于E,过B作BH⊥AD于H,则AE=BH;
同(1),可得∠D=30°,∠DBH=60°.
∵AD∥BC,BH⊥AD,
∴∠HBC=90°;
∴∠DBC=90°+60°=150°.
因此∠DBC的度数为30°或150°.
