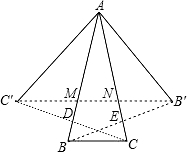
作B点关于AC的对称点B′，作C点关于AB的对称点C′，连接C′B′分别交AB、AC于点M、N，则BN+NM+MC=B′N+MN+MC′为最小值，

∵C′D=CD，C′D⊥AB，

∴△ACC′是等腰三角形，

∴AC′=AC，∠C′AC=∠DAC=20°，

同理，△ABB′是等腰三角形，

∴AB=AB′，∠B′AC=∠BAC=20°，

∵AB=AC，

∴AC′=AB′，

∵∠C′AB′=∠C′AD+∠BAC+∠B′AC=20°+20°+20°=60°，

∴△AB′C′是等边三角形，

∴B′C′=AB′=AB=20cm，即BN+NM+MC的最小值为20cm．

故答案为：20cm．