问题
解答题
等边△ABC中,BD平分∠ABC,延长BC到E,使CE=CD,连接D、E.
(1)求∠E的度数;
(2)小成同学说:BD=DE,她说的对吗?请你说明道理.
(3)把“BD平分∠ABC”改成什么条件,也能得到同样的结论?
答案
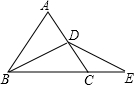
(1)∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°,
∵DC=EC,
∴∠DCE=∠E,
∵∠ACB为△DCE的外角,
∴∠ACB=∠DCE+∠E=2∠E,
则∠E=
∠ACB=30°;1 2
(2)小成同学的说法正确,理由为:
证明:∵∠CBD=∠E=30°,
∴DB=DE;
(3)把“BD平分∠ABC”改成BD⊥AC或BD为AC边上的中线,也能得到同样的结论,
理由为:由AB=BC,BD⊥AC或BD为AC边上的中线,
利用三线合一得到BD平分∠ABC,同(1)(2)得到∠E=30°;DB=DE.
