问题
解答题
证明：等腰三角形底边高上任一点到两腰的距离相等．
答案
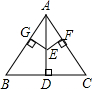
已知：△ABC中，AB=AC，AD⊥BC，点E是AD上任一点，且GE⊥AB，FE⊥AC
求证：GE=EF．
证明：∵△ABC中，AB=AC，AD⊥BC
∴∠BAD=∠CAD
∵GE⊥AB，FE⊥AC
∴GE=EF．
搜题请搜索小程序“爱下问搜题”
证明：等腰三角形底边高上任一点到两腰的距离相等．
已知：△ABC中，AB=AC，AD⊥BC，点E是AD上任一点，且GE⊥AB，FE⊥AC
求证：GE=EF．
证明：∵△ABC中，AB=AC，AD⊥BC
∴∠BAD=∠CAD
∵GE⊥AB，FE⊥AC
∴GE=EF．