问题
问答题
设偶函数f(x)在x=0的邻域内二阶连续可导,且f(0)=1,f"(0)=4.证明:
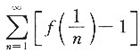 绝对收敛.
绝对收敛.
答案
参考答案:因为f(x)为偶函数,所以f’(-x)=-f’(x),于是f’(0)=0.
因为f(x)在x=0的邻域内二阶连续可导,
所以
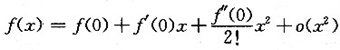 ,即f(x)-1=2x2+o(x2),于是
,即f(x)-1=2x2+o(x2),于是
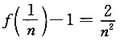
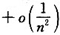 .
.
因为
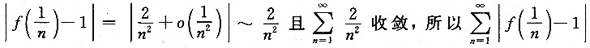 收敛,即
收敛,即
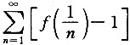 绝对收敛.
绝对收敛.
设偶函数f(x)在x=0的邻域内二阶连续可导,且f(0)=1,f"(0)=4.证明:
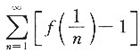 绝对收敛.
绝对收敛.
参考答案:因为f(x)为偶函数,所以f’(-x)=-f’(x),于是f’(0)=0.
因为f(x)在x=0的邻域内二阶连续可导,
所以
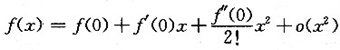 ,即f(x)-1=2x2+o(x2),于是
,即f(x)-1=2x2+o(x2),于是
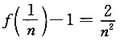
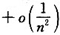 .
.
因为
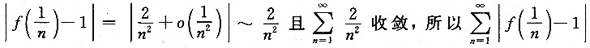 收敛,即
收敛,即
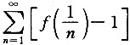 绝对收敛.
绝对收敛.