问题
单项选择题
设函数f(x)在x=0处连续,下列命题错误的是
(A) 若
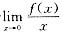 存在,则f(0)=0.
存在,则f(0)=0.
(B) 若
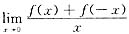 存在,则f(0)=0.
存在,则f(0)=0.
(C) 若
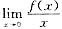 存在,则f′(0)=0.
存在,则f′(0)=0.
(D) 若
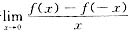 存在,则f′(0)=0.
存在,则f′(0)=0.
答案
参考答案:D
解析: 本题考查可导的极限定义及连续与可导的关系.由于题设条件含有自象函数,本题最简便的方法是用赋值法求解,即取符合题设条件的特殊函数f(x)去进行判断,然后选择正确选项.
取
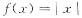 ,则
,则
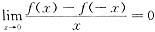 ,但f(x)在x=0不可导,故选(D).
,但f(x)在x=0不可导,故选(D).
事实上,在(A),(B)两项中,因为分母的极限为0,所以分子的极限也必须为0,则可推得f(0)=0.在(C)中,
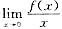 存在,则f(0)=0,f′(0)=
存在,则f(0)=0,f′(0)=
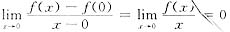 ,所以(C)项正确,故选(D).
,所以(C)项正确,故选(D).
[评注] 对于题设条件含抽象函数或备选项为抽象函数形式结果以及数值型结果的选择题,用赋值法求解往往能收到奇效.
