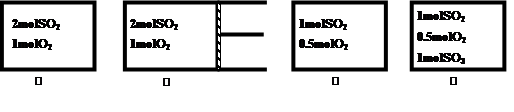问题
问答题
设总体X的概率密度为
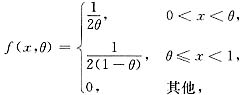
其中参数θ(0＜θ＜1)未知，X1，X2，…，Xn是来自总体X的简单随机样本，
是样本均值．
(Ⅰ)求参数θ的矩估计量
；
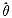(Ⅱ)判断
是否为θ2的元偏估计量，并说明理由．
答案
参考答案：[分析与解答] (Ⅰ)求唯一参数θ的矩估计量
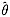，只要令样本均值
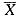等于总体的期望E(X)就可以求得．
现
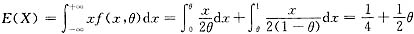，令
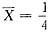
，解得
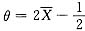．所以参数θ的矩估计量
．
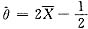(Ⅱ)判断
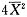是否为θ2的无偏估计量，只要判断
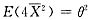是否成立
．
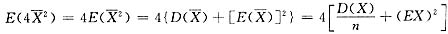由于
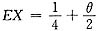，且有
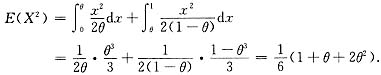
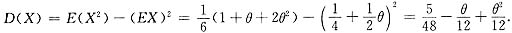
所以，
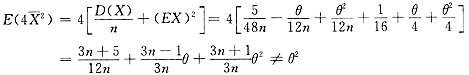
因此，
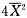不是θ2的元偏估计量．
[评注] (Ⅱ)的计算可简化为
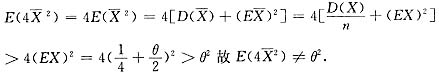
不过这样的验证在考试中是不太容易做到的.
