问题
问答题
证明
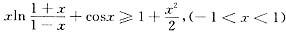 .
.
答案
参考答案:[证明] 令
 ,则
,则
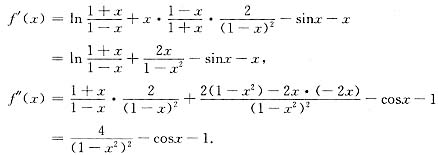
当-1<x<1时,f″(x)≥2>0,所以f′(x)单调增加.于是,
当-1<x<0时,f′(x)<f′(0)=0,于是f(x)在-1<x<0上单调减少,因此有f(x)>f(0)=0,即
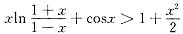
当0<x<1上时,f′(x)>f′(0)=0,于是f(x)单调增加,因此有f(x)>f(0)=0,即
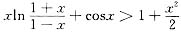
综上所述得,当-1<x<1时,
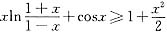 ;(等号在x=0时成立).
;(等号在x=0时成立).
