问题
问答题
设随机变量X的概率密度为
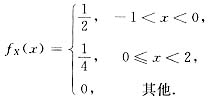
令Y=X2，F(x，y)为二维随机变量(X，Y)的分布函数，求：
(Ⅰ)Y的概率密度fY(y)；
(Ⅱ)
．
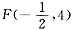答案
参考答案：[分析与解答] (Ⅰ)用定义先求Y的分布函数FY(y)，进而求得fY(y)．已知Y=X2，故FY(y)=P{X2≤y}，当y≤0时FY(y)=0，由题设知
P{-1＜X＜2}=P{-1＜X＜0}+P{0≤X＜2}=1
所以当y＞0时，
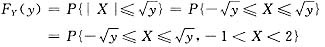
故当
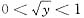，即0＜y＜1．(此时
)
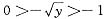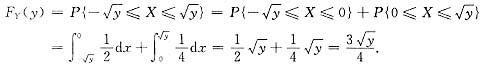
当
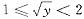，即1≤Y＜4．(此时
)
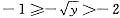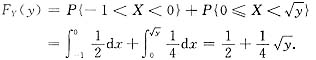
当
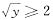，即y≥4(此时
)
FY(y)=P{-1＜X＜2}=1．
综上得
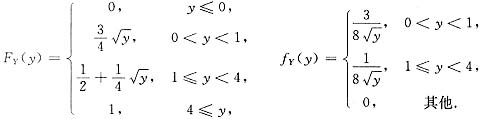
(Ⅱ)
.
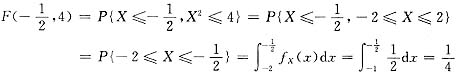[评注] 注意应用P{-1＜X＜2}=1，从而有FY(y)=P{X2≤y，-1＜X＜2}，并借助于图形来确定Y的取值范围．对于概率密度是分段函数的问题，这种确定取值范围的方法经常被用到．