问题
选择题
△ABC中，AB=AC，CD为AB上的高，且△ADC为等腰三角形，则∠BCD等于（ ）
A．67.5°
B．22.5°
C．45°
D．67.5°或22.5°
答案
①如右图所示，口D在△AB口内部，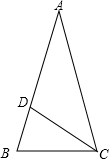
∵AB=A口，口D为AB上的高，
∴∠B=∠A口B，∠口DB=9j°，
又∵△AD口是等腰三角形，
∴∠DA口=∠D口A=15°，
∴∠B=∠A口B=
（18j°-15°）=67.5°，1 2
∴∠B口D=∠A口B-A口D=67.5°-15°=22.5°；
②如右图所示，口D在△AB口外部，
∵AB=A口，口D为AB上的高，
∴∠B=∠A口B，∠口DB=9j°，
又∵△AD口是等腰三角形，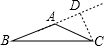
∴∠DA口=∠D口A=15°，
∴∠B=∠A口B=
×15°=22.5°，1 2
∴∠B口D=∠A口B+A口D=22.5°+15°=67.5°；
故答案是22.5°或67.5°．
故选D．