问题
解答题
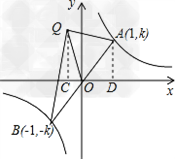
在平面直角坐标系内，反比例函数和二次函数y=k（x2+x﹣1）的图象交于点A（1，k）和点B（﹣1，﹣k）．
（1）当k=﹣2时，求反比例函数的解析式；
（2）要使反比例函数和二次函数都是y随着x的增大而增大，求k应满足的条件以及x的取值范围；
（3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．
答案
解：（1）当k=﹣2时，A（1，﹣2），
∵A在反比例函数图象上，
∴设反比例函数的解析式为：y=
，
代入A（1，﹣2）得：﹣2=
，
解得：m=﹣2，
∴反比例函数的解析式为：y=﹣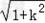
；
（2）∵要使反比例函数和二次函数都是y随着x的增大而增大，
∴k＜0，
∵二次函数y=k（x2+x﹣1）=k（x+
）2﹣
k的对称轴为：
直线x=﹣
，
要使二次函数y=k（x2+x﹣1）满足上述条件，
在k＜0的情况下，x必须在对称轴的左边，
即x＜﹣
时，才能使得y随着x的增大而增大，
∴综上所述，k＜0且x＜﹣
；
（3）由（2）可得：Q（﹣
，
k），
∵△ABQ是以AB为斜边的直角三角形，
A点与B点关于原点对称，（如图是其中的一种情况）
∴原点O平分AB，
∴OQ=OA=OB，
作AD⊥OC，QC⊥OC，
∴OQ=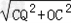
=
，
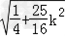∵OA=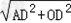
=，
∴
=
，
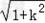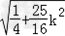解得：k=±
．
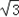