问题
选择题
在钝角三角形ABC中，若AB=AC，D是BC上一点，AD把△ABC分成两个等腰三角形，则∠BAC的度数为（ ）
A．150°
B．124°
C．120°
D．108°
答案
设∠ABC为x．
（180°-x）÷2+x+2x=180°
解得x=36°
∴180°-36°×2=108°．
故选D．
搜题请搜索小程序“爱下问搜题”
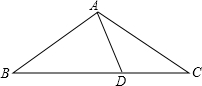
在钝角三角形ABC中，若AB=AC，D是BC上一点，AD把△ABC分成两个等腰三角形，则∠BAC的度数为（ ）
A．150°
B．124°
C．120°
D．108°
设∠ABC为x．
（180°-x）÷2+x+2x=180°
解得x=36°
∴180°-36°×2=108°．
故选D．