问题
选择题
已知等腰三角形有一个角是40°,那么它腰上的高线和底边的夹角是( )
A.20°
B.50°
C.20°或50°
D.大小无法确定
答案
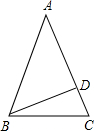
当40°的角是顶角时:
∴∠ACB=
=70°180-40 2
在直角△BCD中,∠CBD=90°-70°=20°;
当40°的角是底角时,
即∠ACB=40°,
在直角△BCD中,∠CBD=90°-∠ACB=50°,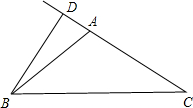
故腰上的高线和底边的夹角是20°或50°.
故选C.