A、∵三角形中，2个内角是70°与40°，

∴第三个内角为180°-（70°+40°）=70°，

∴三角形中有两个角相等，都为70°，

则此三角形为等腰三角形，本选项不合题意；

B、一个外角的平分线平行于一边的三角形是等腰三角形，理由如下：

如图所示：AD为△ABC外角∠EAC的平分线，∴∠EAD=∠DAC，

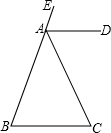
又AD∥BC，

∴∠EAD=∠B，∠DAC=∠C，

∴∠B=∠C，

∴AB=AC，即三角形ABC为等腰三角形，本选项不合题意；

C、有2个内角不等的三角形不一定是等腰三角形，也可以为等腰三角形，

例如：在△ABC中，∠A=∠C=50°，∠B=80°，

其中∠A≠∠B，但是∠A=∠C，可得出BA=BC，

此时三角形ABC为等腰三角形，本选项符合题意；

D、有2个不同顶点的外角相等的三角形是等腰三角形，理由为：

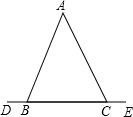
已知：∠ABD与∠ACE为△ABC的外角，且∠ABD=∠ACE，

求证：△ABC为等腰三角形，

证明：∵∠ABD+∠ABC=180°，∠ACE+∠ACB=180°，

且∠ABD=∠ACE，

∴∠ABC=∠ACB，

∴AB=AC，即△ABC为等腰三角形，本选项不合题意．

故选C