参考答案：C

解析：

首先，应确定这是一个组合类题。先将9个数进行奇、偶数分类，其中1、3、5、7、9为奇数，2、4、6、8为偶数。要使任取3个数的和为偶数，则要求3个数全是偶数，或者是取1个偶数和2个奇数。具体步骤可分为两类: (1)3个全是偶数的取法。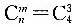=4(种)； (2)1个偶数，2个奇数的取法。=4×10=40(种)。 所以总的取法是一类的4加上二类的40，即4+40=44(种)。故选C。