问题
解答题
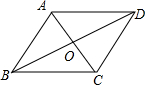
已知四边形ABCD，连接AC、BD交于点O，且满足条件：AB+DC=AD+BC，AB2+AD2=BC2+DC2，
（1）若AB=AD，求证：∠BAC=∠BCA；
（2）若AB＞AD，当OD绕点O逆时针旋转180°时，点D能否落在线段OB上，并说明理由．
答案
（1）证明：∵AB+DC=AD+BC，AB=AD，
∴DC=BC，
∵AB2+AD2=BC2+DC2，
∴AB=AD=BC=DC，
∴∠BAC=∠BCA；
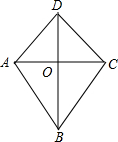（2）当OD绕点O逆时针旋转180°时，点D能落在线段OB上．
∵AB2+AD2=BC2+DC2，
∴AB2-DC2=BC2-AD2，
∴（AB+DC）（AB-DC）=（AD+BC）（BC-AD），
∵AB+DC=AD+BC，
∴AB-DC=BC-AD，
∴AB=BC，DC=AD，
∴BD垂直平分AC，且OB＞OD，
∴当OD绕点O逆时针旋转180°时，点D能落在线段OB上．
