问题
解答题
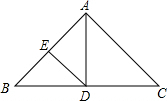
等腰△ABC中，AB=AC=8，∠BAC=100°，AD是BC边上的中线，交BC于D，点E是AB的中点，连接DE．
（1）求∠BAD的度数；
（2）求∠BED的度数；
（3）求线段DE的长．
答案
（1）∵AD是BC边上的中线，
∴∠BAD=∠CAD，
∵∠BAC=100°，
∴∠BAD=50°；
（2）∵AB=AC，
∴∠B=∠C，∠ADB=90°，
∴∠B=（180°-100°）÷2=40°，
∵点E是AB的中点，
∴BE=DE，
∴∠BDE=40°，
∴∠BED=180°-40°×2=100°；
（3）∵AB=AC，AD是BC边上的中线，
∴AD是等腰△ABC底边BC上的高，即∠ADB=90°，
在直角三角形ABD中，点E是AB的中点，
∴DE为斜边AB边上的中线，
∴DE=
AB=4．1 2
，速度方向与x轴负方向夹角θ＝30º. 质子第一次到达y轴时速度方向与y轴垂直，第三次到达y轴的位置用B点表示，图中未画出，已知OA＝l，不计质子重力影响. 