问题
问答题
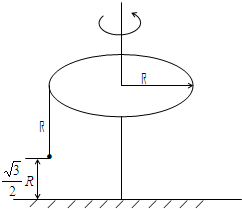
如图所示,水平圆盘半径为R,可绕过圆盘中心的竖直轴转动,在圆盘的边缘用长为R的细线拴着质量为m的小球,圆盘静止时小球离地面高度为
R,拴小球的细线能承受的最大拉力为3 2 2 3
mg,现让圆盘转动的角速度缓慢增加,求:①细线欲断不断时圆盘转动的角速度为多大?②细线断开后小球落地点到转轴的距离为多少?(结果保留根号)3
答案
(1)设细线的拉力恰好达到最大时与竖直方向的夹角为α,此时,小球圆周运动的半径为r=R+Rsinα.

∵cosα=
=mg T
∴α=30°,所以r=3 2
R3 2
根据牛顿第二定律得
mgtan30°=mω2r
解得ω=1 3 2
g3 R
(2)细线断开后小球做平抛运动,初速度为v=ωr=2
gR3 2
高度h=R+
R-Rcos30°=R3 2
则平抛运动的时间为t=
,水平位移x=vt2R g
R3
根据几何知识得到,细线断开后小球落地点到转轴的距离为
S=
=x2+(1.5R)2
R
+3 9 4
答:
①细线欲断不断时圆盘转动的角速度为ω=1 3
.2
g3 R
②细线断开后小球落地点到转轴的距离为
R.
+3 9 4
