问题
证明题
已知△ABC中,∠B=2∠A,AB=2BC。
求证:△ABC是直角三角形。
答案
证明:作AB的中垂线DE,交AC于D,交AB于E,连结BD。
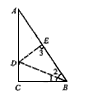
因为DE⊥AB,AE=BE
所以AD=BD
所以∠2=∠A
因为∠ABC=2∠A
所以∠1=∠2
因为AB=2BC
所以BE=BC
所以△EDB≌△CDB
所以∠C=∠3=Rt∠
所以△ABC是直角三角形。
已知△ABC中,∠B=2∠A,AB=2BC。
求证:△ABC是直角三角形。
证明:作AB的中垂线DE,交AC于D,交AB于E,连结BD。

因为DE⊥AB,AE=BE
所以AD=BD
所以∠2=∠A
因为∠ABC=2∠A
所以∠1=∠2
因为AB=2BC
所以BE=BC
所以△EDB≌△CDB
所以∠C=∠3=Rt∠
所以△ABC是直角三角形。