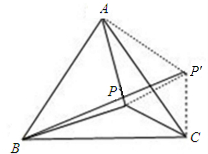
如图，作P关于AC的对称点P′，连接AP′、P′C、PP′，

则P′C=PC，ACP′=∠ACP．

∵AB=AC，∠BAC=80°，

∴∠ABC=∠ACB=50°，

又∵∠PBC=10°，∠PCB=20°，

∴∠BPC=150°，∠ACP=30°，∠ACP′=30°，

∴∠PCP′=60°，

∴△PCP′是等边三角形，

∴PP′=PC，∠P′AC=∠PAC，∠P′PC=60°，

∴∠BPP′=360°-150°-60°=150°，

∴∠BPP′=∠BPC，

∴△PBP′≌△PBC，

∴∠PBP′=∠PBC=10°，

∴∠P′BC=20°，∠ABP′=30° 又∠ACP′=30°，

∴∠ABP′=∠ACP′，

∴A、B、C、P′四点共圆，

∴∠PAC=∠P′AC=∠P′BC=20°，

∴∠PAB=60°．

故选B．