问题
问答题
轻杆AB长2L,A端连在固定轴上,B端固定一个质量为2m的小球,中点C固定一个质量为m的小球,AB杆可以绕A端在竖直平面内自由转动,现将杆置于水平位置,如图所示,然后由静止释放,不计各处摩擦与空气阻力,试求:
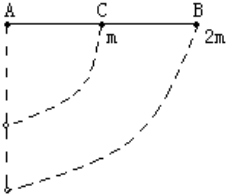
(1)AB杆转到竖直位置时,角速度ω多大?
(2)AB杆转到竖直位置的过程中,B端小球的机械能增量多大?
答案
(1)在转动过程中,A、B两球的角速度相同,设C球的速度为vC,B球的速度为vB,则有
vC=
vB 1 2
以A、B和杆组成的系统机械能守恒,由机械能守恒定律,并选最低点为零势能参考平面,则有
E1=mg•L+2mg•2L=5mgL,
E2=mgL+
m1 2
+v 2C
2m1 2 v 2B
又E1=E 2
以上四式联立可以求出:vB=2 10gL 3
由公式:vB=ω•2L
解得:ω=10g 9L
(2)B端小球的机械能增量:△E=
2m1 2
-2mg•2L=v 2B
mgL4 9
答:AB杆转到竖直位置时,角速度ω=
;B端小球的机械能增量10g 9L
mgL.4 9
