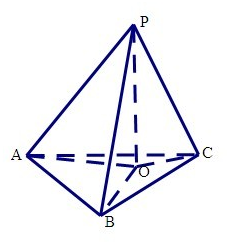
过三角形ABC所在平面外的一点P，作PO⊥平面α，垂足为O，连PA、PB、PC，

若PA=PB=PC，连接OA，OB，OC，则OA=OB=OC，则O为三角形ABC的外心；又若∠C=90°，则O为AB的中点．

故①②正确．

若PA⊥PB，PB⊥PC，PC⊥PA，则PA⊥平面PBC，从而PA⊥BC，

又PO⊥平面ABC，则PO⊥BC，所以BC⊥平面PAO，从而BC⊥AO，

同理AB⊥CO，AC⊥BO，故O为三角形的垂心，故③错，应改为垂心．

故选：B