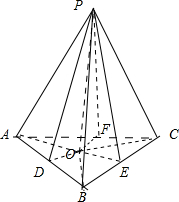
已知P是△ABC所在平面α外一点,O是点P在平面α内的射影
(1)若P到△ABC的三个顶点的距离相等,则O是△ABC外心;
(2)若PA、PB、PC与平面α所成的角相等,则O是△ABC的内心;
(3)若P到△ABC三边距离相等,且O在△ABC的内部,则O是△ABC的内心;
(4)若平面PAB、PBC、PCA与平面α所成的角相等,且O在△ABC的内部,则O是△ABC的外心;
(5)若PA、PB、PC两两垂直,则O是△ABC的垂心.
其中正确命题的序号是______(把你认为正确命题的序号都写上)
对于(1),如图P是△ABC所在平面外一点,O是P点在平面a上的射影.
若P到△ABC三个顶点的距离相等,由条件可证得OA=OB=OC,
由三角形外心的定义可知,此时O是三角形ABC的外心,
∴命题(1)正确;
对于(2),∠PAO=∠PBO=∠PCO⇒AO=BO=CO⇒O为三角形的外心,
∴命题(2)不正确.
对于(3),在△ABC内部取一点P使得点P到△ABC的三边距离相等,
∴点P应是△ABC的三内角角平分线的交点.三内角角平分线的交点,则O是△ABC的内心,
∴命题(3)正确;
对于(4),∠PEO=∠PFO=∠PDO⇒OD=OE=OF⇒O为三角形的内心.则O是△ABC的外心,命题(4)不正确.
对于(5),连结AO并延长,交BC与D连结BO并延长,交AC与E;
因PA⊥PB,PA⊥PC,故PA⊥面PBC,故PA⊥BC;
因PO⊥面ABC,故PO⊥BC,故BC⊥面PAO,
故AO⊥BC即AD⊥BC;
同理:BE⊥AC;
故O是△ABC的垂心.
∴命题(5)正确;
故答案为:(1)(3)(5).