问题
解答题
在△ABC中，∠C=90°，AC=2.1 cm，BC=2.8 cm
（1）求这个三角形的斜边AB的长和斜边上的高CD的长；
（2）求斜边被分成的两部分AD和BD的长。
答案
解：（1）∵△ABC中，∠C=90°，AC=2.1 cm，BC=2.8 cm
∴AB2=AC2+BC2=2.12+2.82=12.25 ∴AB=3.5 cm
∵S△ABC=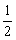
AC·BC=
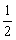AB·CD
∴AC·BC=AB·CD
∴CD=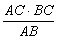
=
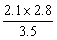=1.68(cm)；
（2）在Rt△ACD中，由勾股定理得： AD2+CD2=AC2
∴AD2=AC2-CD2=2.12-1.682 =(2.1+1.68)(2.1-1.68) =3.78×0.42=2×1.89×2×0.21 =22×9×0.21×0.21
∴ AD=2×3×0.21=1.26(cm)
∴BD=AB-AD=3.5-1.26=2.24(cm)