问题
解答题
设A={x|x2+4x=0}，B={x|x2+2（a+1）x+a2-1=0}，若A∩B=B，求a的值。
答案
解：对B进行分类讨论：
（1）若B≠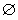
，则B
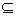A，
设0∈B，则a2-1=0，解得：a=±1；
当a=-1时，B={0}符合题意；
当a=1时，B={0，-4}符合题意；
设-4∈B，则a=1或a=7，
当a=7时，B={-4，-12}不符合题意；
（2）若B=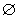
，则x2-2（a+1）x+a2-1=0，
此时△＜0，得a＜-1；
综上所述，a的取值范围是a≤-1或a=1。