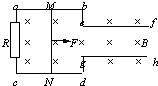
如图所示,电阻不计的光滑导轨abef和cdgh固定在同一水平面上.ab与cd间距为L,ef与gh间距为
,a、c间接一阻值为R的电阻.磁感强度为B的匀强磁场垂直导轨平面,导体棒MN长为L、质量为m、L 2
电阻也为R,搁在左边宽导轨上,在垂直于导体棒的水平
恒力F作用下恰匀速向右滑动,从进入窄导轨起,当滑过
距离S后,导体棒MN又达到匀速运动.试求:
(1)导体棒开始时匀速滑动的速度;
(2)导体棒从进入窄导轨起直至又达到匀速运动的过程中导体棒将做什么运动?并求出此过程中通过电阻R的电量;
(3)在上述(2)的过程中,电流所做的功.
(1)导体棒开始时产生的感应电动势?1=BLv1,
感应电流 I1=
,?1 2R
安培力FA=BI1L,
因导体棒匀速运动,则有FA=F
联立以上各式解得 v1=2FR B2L2
(2)导体棒进入窄轨道后,F>F安,做加速度减小的变加速运动,当F=F安时,开始匀速运动,速度最大.
此过程中通过电阻R的电量 q=
t=. I
=
t. ? R
=△φ R
=BLS R+ R 2
.2BLS 3R
(3)导体棒进入窄轨道后产生感应电动势 ?2=
,Bv2L 2
感应电流 I2═
= ?2 R+ R 2
,2 ?2 3R
安培力FA′=BI2L 2
由平衡条件得:F=FA′,得v2=6FR B2L2
(3)由动能定理:FS-W电=
mv1 2
- 22
mv1 2 21
解得 W电=FS-16mF2R2 B4L4
答:
(1)导体棒开始时匀速滑动的速度为
;2FR B2L2
(2)导体棒从进入窄导轨起直至又达到匀速运动的过程中导体棒做加速度减小的变加速运动,此过程中通过电阻R的电量
;2BLS 3R
(3)在上述(2)的过程中,电流所做的功为FS-
.16mF2R2 B4L4
