问题
解答题
设A={x|x2+4x=0}，B={x|x2+2（a+1）x+a2-1=0} ，其中x∈R，如果A∩B=B，求实数a的取值范围。
答案
解：由A∩B=B，得B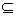
A，
而A={-4，0}，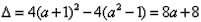
，
当△=8a+8＜0，即a＜-1时，B=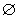
，符合B
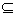A；
当△=8a+8=0，即a=-1时，B={0}，符合B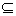
A；
当△=8a+8＞0，即a＞-1时，B中有两个元素，而B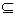
A={-4，0}，
∴B={-4，0}，得a=1；
综上，a=1或a≤1。