（1）∵一次函数和反比例函数的图象交于点（4，m），∴有

m=-4k+8 m= k 4

，

解之得

m=4 k=16

，

∴m=4，k=16；

（2）若两个函数相交，则交点坐标满足方程组

y= k x (k≠0) y=-x+8

，

∴-x+8=

k

x

，

即x²-8x+k=0，

要使两个函数有两个不同的交点，则方程应有两个不相同的根，

也就是△＞0，

即（-8）²-4×1×k=64-4k＞0，

∴k＜16，

∴要使两个函数图象有两个不同交点，k应满足k＜16且k≠0；

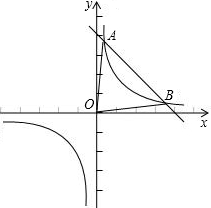
（3）当0＜k＜16时，y=

k

x

的图象在第一、三象限，它与y=-x+8的两个交点都在第一象限内，这时∠AOB是锐角；

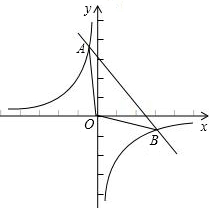
当k＜0时，y=

k

x

的图象在第二、四象限，它与y=-x+8的两个交点分别在第二、四象限，此时∠AOB是钝角．