（1）由题意得1=

k

- 3

，解得k=-

3

，

∴反比例函数的解析式为y=-

3

x

；

（2）过点A作x轴的垂线交x轴于点C．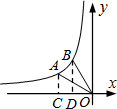

在Rt△AOC中，OC=

3

，AC=1，

∴OA=

OC2+AC2

=2，∠AOC=30°，

∵将线段OA绕O点顺时针旋转30°得到线段OB，

∴∠AOB=30°，OB=OA=2，

∴∠BOC=60°．

过点B作x轴的垂线交x轴于点D．

在Rt△BOD中，BD=OB•sin∠BOD=

3

，OD=

1

2

OB=1，

∴B点坐标为（-1，

3

），

将x=-1代入y=-

3

x

中，得y=

3

，

∴点B（-1，

3

）在反比例函数y=-

3

x

的图象上．

（3）由y=-

3

x

得xy=-

3

，

∵点P（m，

3

m+6）在反比例函数y=-

3

x

的图象上，其中m＜0，

∴m（

3

m+6）=-

3

，

∴m²+2

3

m+1=0，

∵PQ⊥x轴，∴Q点的坐标为（m，n）．

∵△OQM的面积是

1

2

，

∴

1

2

OM•QM=

1

2

，

∵m＜0，∴mn=-1，

∴m²n²+2

3

mn²+n²=0，

∴n²-2

3

n=-1，

∴n²-2

3

n+9=8．