问题
填空题
已知⊙O的半径为r,弦AB=
|
答案
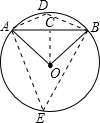
根据题意画出相应的图形,
过O作OC⊥AB,D、E为圆周上的点,连接AD,BD,AE,BE,
可得C为AB的中点,即AC=BC=
AB=1 2
r,2 2
∵OA=OB=r,AC=BC=
r,2 2
∴△AOC与△BOC都为等腰直角三角形,
∴∠AOC=∠BOC=45°,
∴∠AOB=90°,
∴∠AEB=45°,∠ADB=135°,
则AB所对的圆周角的度数为45°或135°.
故答案为:45°或135°
