问题
解答题
设A={（x，y）|y=-4x+6}，B={（x，y）|y=5x-3}，求A∩B。
答案
解：A∩B的元素就是集合A与集合B所表示的方程所组成的方程组的解构成的，或者看成直线y=-4x+6和直线y=5x-3的交点
∵
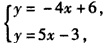
解得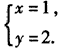
∴A∩B={（x，y） |y=-4x+6} ∩ {（x，y） |y=5x-3}={（1，2）}。
搜题请搜索小程序“爱下问搜题”
设A={（x，y）|y=-4x+6}，B={（x，y）|y=5x-3}，求A∩B。
解：A∩B的元素就是集合A与集合B所表示的方程所组成的方程组的解构成的，或者看成直线y=-4x+6和直线y=5x-3的交点
∵
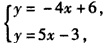
解得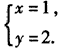
∴A∩B={（x，y） |y=-4x+6} ∩ {（x，y） |y=5x-3}={（1，2）}。