问题
选择题
在△ACD中,AB⊥CD,垂足为B,且BD>CB,E为AB上任一点,△BCE和△ABD都是等腰直角三角形中,下列结论正确的是( )
A.△ABC≌△DBE
B.△ACB≌△ABD
C.△CBE≌△BED
D.△ACE≌△ADE
答案
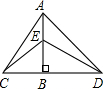
A、∵AB⊥CD,
∴∠ABC=∠ABD=90°,
∵△BCE和△ABD都是等腰直角三角形,
∴BC=BE,BA=BD,
∴△ABC≌△DBE,故本选项正确;
B、∵△ABC≌△DBE,
∴△ACB的面积小于△ABD的面积,
故本选项错误;
C、同理△BCE的面积小于△BED的面积,故本选项错误;
D、AB=AB,BD>BC,根据勾股定理可得:AC≠AD,即△ACE和△ADE不全等,故本选项错误;
故选A.
