问题
填空题
正方形ABCD的边长为2,以CD为斜边作等腰直角三角形PCD,则S△ABP为______.
答案
①当点P在正方形的外部时,过点P作PE⊥AB于E,交DC于F,
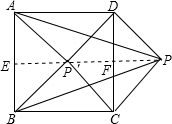
∵△PCD是以CD为斜边作等腰直角三角形,
∴PD=PC.DC=2,
∴PF=
DC=1,1 2
∵PE=EF+PF=2+1=3,
∴S△ABP=
×AB?PE=1 2
×2×3=3;1 2
②当点P在正方形的内部时,
P′E=
AB=1,AB=2,1 2
∴S△ABP,=
×AB×P′E=1 2
×2×1=1,1 2
故答案为:1或3.
