问题
选择题
下列说法正确的是( )
A.等腰梯形既是中心对称图形,又是轴对称图形
B.矩形是轴对称图形,有四条对称轴
C.等腰三角形一腰上的高与底边的夹角等于顶角的一半
D.有一个角的平分线平分对边的三角形是等腰直角三角形
答案
A、等腰梯形不是中心对称图形,是轴对称图形,故本选项错误;
B、矩形是轴对称图形,对称轴是过对边中点的直线,共2条,故本选项错误;
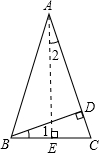
C、如图,过点A作AE⊥BC,则AE平分∠BAC,
∴∠2=
∠A,1 2
∵BD⊥AC,
∴∠1+∠C=90°,
又∠2+∠C=90°,
∴∠1=∠2,
∴∠1=
∠A,1 2
即等腰三角形一腰上的高与底边的夹角等于顶角的一半,故本选项正确;
D、有一个角的平分线平分对边的三角形是等腰三角形,不一定是等腰直角三角形,故本选项错误.
故选C.
